北航太阳成集团tyc7111cc学术报告

及偏微分方程讨论班

题目: Stability of rarefaction wave for stochastic Burgers equation

报告人：黄飞敏 研究员(中国科学院)

报告时间：2020年12月14日下午15:00-16:00(北京时间)

腾讯ID：884 604 022 密码：123456

摘要: The large time behavior of strong solutions to the stochastic Burgers equation is considered in this paper. It is first shown that the unique global strong solution to the one dimensional stochastic Burgers equation time-asymptotically tend to a rarefaction wave provided that the initial data 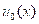satisfies 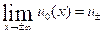and 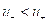, that is, the rarefaction wave is non-linearly stable under white noise perturbation for stochastic Burgers equation. A time-convergence rate is also obtained. Moreover, an important inequality (denoted by Area Inequality) is derived. This inequality plays essential role in the estimates, and may have applications in the related problems, in particular for the time-decay rate of solutions of both the stochastic and deterministic PDEs. As an application, the stability of planar rarefaction wave is shown stable for a two dimensional viscous conservation law with stochastic force.

报告人简介：黄飞敏、中科院数学院华罗庚首席研究员，杰青，主要从事偏微分方程的理论研究，在双曲守恒律方程组和粘性守恒律方程组取得了一系列重要的研究成果。他已在Adv. Math, CMP, ARMA等著名数学刊物上发表学术论文90余篇，引用次数1700余次。曾获得国家自然科学奖二等奖、美国工业与应用数学学会杰出论文奖。

邀请人：郑孝信