2020年6月3日下午,我院计算科学系“青年教师科研工作论坛”于腾讯会议线上举办。会议由计算科学系系主任冯仁忠老师主持。
本期论坛邀请了计算科学系八位青年教师进行了交流报告。与会教师就感兴趣的学术问题进行了交流,探索合作契机。




“青年教师科研工作论坛”的创建,旨在为我院青年教师和同学提供一个科研工作交流的平台,对国际前沿和热点问题进行分享,从而进一步促进科研工作的开展和科研水平的提高。“青年教师科研工作论坛”将会持续开展下去!欢迎我院教师和同学们积极参加!
报告一
报告题目:The Refined FEAST Method And Its BackwardStability Analysis
报告摘要: Thispaper proposes a new method called the Refined FEAST method based on the FEASTalgorithm. The FEAST algorithm is a subspace iteration method for solvingeigenvalue problems. But it has the same problems as traditional methods thatis the Ritz vector may fail to converge. The refined eigenvector of the newmethod can overcome this problem. It can unconditionally converge to thedesired eigenvector with the convergence of the subspace. The analysis showsthat the new method has better numerical stability than the original FEASTmethod. Finally, we use numerical experiments to confirm the theory results.
报告人简介:孙玉泉,太阳成集团tyc7111cc,副教授,硕士生导师。主要研究领域为矩阵计算及在人工智能相关领域的应用研究。
代表作:
1.Liu Yang, Yuquan Sun *, Fanghui Gong, The inexact residual iteration method forquadratic eigenvalue problem and the analysis of convergence, Journal ofComputational and Applied Mathematics, 2018(2).
2.Gong F H, Sun Y Q. A new shift strategy for the implicitly restartedgeneralized second-order Arnoldi method (in Chinese). Sci Sin Math, 2017, 47:635-650.
3. Ovchinnikov, Yuquan Sun,Enßlin, Torsten A, et al. Supersymmetric theory of stochastic ABC model[J].Journal of Physics Communications, 2018, 2(6).

报告二
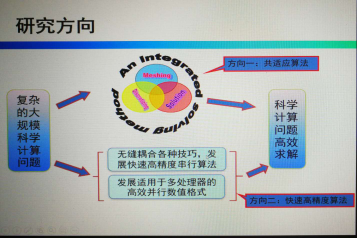
报告题目:飞行器结构优化中敏度分析的一种快速算法
报告摘要: 飞行器结构优化中位移和应变敏度的高效计算是制约整个算法计算效率的技术瓶颈。针对飞行器结构优化问题,充分利用问题中稀疏矩阵的特点,通过综合运用随机奇异值分解、SuperLU和扩展的SMW算法等技术,发展了一种针对飞行器结构优化中位移和应变敏度计算的快速算法。数值结果表明所发展的求解器的有效性和高效性。
报告人简介:朱立永,2007年于中国科学院数学与系统科学研究院取得理学博士学位。 2009年入职北航数学与系统科学学院任讲师,2015年任计算科学系副教授。研究方向:高性能算法及其在科学工程中的应用。感兴趣的领域:有限元,快速算法,并行计算,网格生成、人工智能等。
代表作:
1. Qiang Du, Desheng Wang and Liyong Zhu,On Mesh Geometry and Stiffness Matrix Conditioning for General Finite ElementSpaces, SIAM Journal of Numerical Analysis, 47(2009), 1421-1444.
2. Liyong Zhu and Qiang Du, Meshdependent stability and condition number estimates for finite element approximationsof parabolic equations, Mathematics of Computation, 83 (2014), 37-64.
3. Liyong Zhu, Lili Ju, Weidong Zhao,Fast High-Order Compact Exponential Time Differencing Runge–Kutta Methods forSecond-Order Semilinear Parabolic Equations, Journal of Scientific Computing,67(2016),1043–1065.

报告三
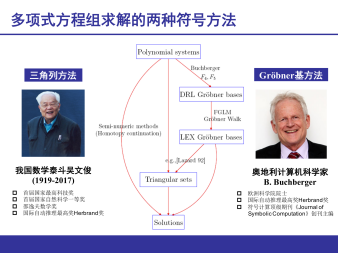
报告题目: 多项式系统的符号求解
报告摘要: 在本报告中,我将围绕着多项式系统求解这一符号计算领域的核心研究问题简述个人的学术进展,主要包括:(1)用于Groebner基换序的高效稀疏FGLM算法;(2)基于弦图理论的自上而下形式的三角分解研究;(3)融合Groebner基和三角列的特征分解理论。
报告人简介:牟晨琪,男,太阳成集团tyc7111cc讲师。他的主要研究领域是符号计算,特别是利用三角列和Groebner基等代数工具来求解多项式系统及其应用。他目前是期刊《Journal ofSystems Science and Complexity》、《系统科学与数学》编委,以程序委员会副主席、组委会联合主席等身份参与组织了CM2020和ISSAC2019等多项国内外学术活动。
代表作:
1.J.-C. Faugère and C. Mou. Sparse FGLMalgorithms. Journal of Symbolic Computation, 80: 538-569, 2017.
2. C. Mou, Y. Bai, and J. Lai.Chordal graphs in triangular decomposition in top-down style. Journal ofSymbolic Computation, in press.
3. D. Wang, R. Dong, and C.Mou. Decomposition of polynomial sets into characteristic pairs. Mathematics ofComputation, 89: 1993-2015, 2020.
报告四
报告题目:基于深度学习的数学推理与计算
报告摘要:从莱布尼兹时代以来,用机器证明数学定理是数学家和计算机科学家的梦想,以符号逻辑和符号计算为基础的形式方法在过去半个多世纪取得了很大成功。然而,这类方法的实现依赖于人工设置的证明策略(即决定采取怎样的证明步骤),这需要人的经验、直觉和洞察力。近年来,以深度学习为代表的人工智能技术在识别和感知等诸多领域取得了巨大成功;另一方面,人们积累了大量的数学证明和计算数据。基于这两方面,我们探索如何利用深度学习技术让机器从数据中学会推理和计算,研究数学概念、公式、命题的表示学习方法,设计有效的学习模型来捕获人类证明经验,实现不断自我完善的定理自动证明系统。
报告人简介:陈肖宇,博士毕业于北航数学学院,师从王东明教授,从事数学知识管理与几何自动推理的研究。荷兰埃因霍温理工大学访问学者,北航软件开发环境国家重点实验室博士后,ADG、ICMS、KMIS、MACIS等系列国际会议的程序委员会委员,MCS期刊客座编辑,主持国家自然科学基金1项。研究兴趣包括深度学习、自动推理、知识管理。
代表作:
1. Retrieving geometric information from images:the case of hand-drawn diagrams. Data Mining and Knowledge Discovery 31(4):934–971, 2017。

报告五
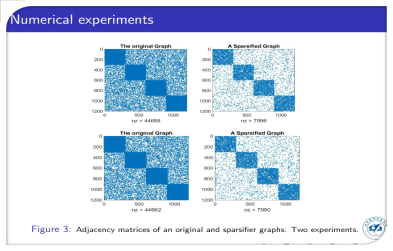
报告题目:稀疏逼近的一些算法与理论
报告摘要:将简要介绍本人的一些研究工作。包括能应用于求解稀疏信号恢复问题的加速的交替极小化方法,交错多项式族工具及其应用,图的稀疏谱逼近等。
报告人简介:谢家新,2019年于中国科学院数学与系统科学研究院博士后出站,2019年入职航。主要研究兴趣是数据科学中的数学问题,特别是具有稀疏性特点问题的理论,算法及应用。
代表作:
1. JiaxinXie, ZhiqiangXu, Subset selection for matrices with fixed blocks, arXiv:1903.06350.
2. Yuan Lei, JiaxinXie, A symmetric alternating minimization algorithm for total variationminimization, arXiv: 2002.09180, to appear in Signal Processing
3. JiaxinXie, A note on restricted invertibility with weighted columns,arXiv: 2005.01070.

报告六
报告题目: Exact boundary conditions of 1D nonlocalSchrödinger equations and its numerical analysis
报告摘要: A general method is proposed to constructexact artificial boundary conditions (ABCs) for the 1D non-local Schrödingerequation and non-local heat equation. The stability and the convergent rate areproved rigorously. The method canbe applied to modeling of wave propagation of general non-local theories andhigh dimensional cases.
报告人简介:庞刚,2013年在北京大学获得博士学位,2019年入职北航,主要研究方向为偏微分方程的数值边界条件。
代表作:
1. Accurateartificial boundary conditions for the semi-discretized linear Schrödinger andheat equations on rectangular domains. Computer Physics Communications, 2018,22:84-93.
2. ALmost EXactboundary conditions for transient Schrdinger-Poisson system. Journal ofComputational Physics, 2016, 313: 233-246.
3. Approximatelinear relations for Bessel functions. Communications in Mathematical Sciences,2017,15:1967-1986.

报告七
报告题目: 多元多项式矩阵分解研究
报告摘要: 多元多项式矩阵的分解问题主要来源于多维系统、信号处理等工程领域。多元多项式矩阵分解是指将一个矩阵分解为若干个矩阵的乘积,并满足一定的关系。在本次报告中,我将简要介绍多元多项式矩阵分解的具体问题,以及相关工作进展。
报告人简介:鲁东,博士后,2019年6月于中国科学院数学与系统科学研究院获得博士学位,师从王定康研究员;2019年7月进入北航太阳成集团tyc7111cc从事博士后研究工作,合作导师是王东明教授。研究领域为符号计算,具体方向有多元多项式矩阵分解与等价问题研究、签名Gröbner基算法的理论研究、参数Gröbner系统算法的应用等。
代表性成果:
1. Kapur D., Lu D., MonaganM., Sun Y., Wang D., Algorithms for computing greatest common divisors ofparametric multivariate polynomials. Journal of Symbolic Computation(2019), .
2. Lu D., Wang D., Xiao F., Zhou J., Extending the GVW algorithmto local ring. In proceedings of 43rd ISSAC, 271-278, 2018.
3. Lu D., Ma X., Wang D., Anew algorithm for general factorizations of multivariate polynomial matrices. Inproceedings of 42nd ISSAC, 277-284, 2017.

报告八
报告题目: 格理论的研究及其应用
报告摘要:首先我们给出有限格维数的概念及其特性。我们得到有限格的维数集就是自然数集,并且维数对于格代数各种运算具有保持性。运用有限格维数的特性,我们解决了两个关于格的覆盖维数的公开问题。接下来我们基于完备格理论以及模糊算法,提出了一种全新的针对彩色图像的边缘检测算法。
报告人简介:张海峰,女,1985年生,内蒙古人。太阳成集团tyc7111cc数学与系统科学学院博士后。主要研究方向:格代数理论及其应用。
代表作:
1. Hai-feng Zhang, Meng Zhou, Guang-junZhang. Correction to “A study of covering dimension for the class of finite lattices” [Discrete Mathematics 338 (2015) 1096–1110].[J] Discrete Mathematics, Volume 339, Issue 6, 6 June 2016, Pages 1722-1723.
2. Hai-feng Zhang, Meng Zhou, Guang-junZhang. Answer to some open questions on covering dimension for finite lattices,[J] Discrete Mathematics, Volume 340, Issue 5, May 2017, Pages 1086-1091.

